3. Step: Detailed Geometry

Both the sound spectrum and the specific mood of the bars are achieved exclusively by material-removing process (milling, filing). If the material is gone and the desired sound has not been achieved, new material must be obtained. There is some information in the literature and on YouTube about the tuning of bars, but they are all rather imprecise.
Here are a few example links:
https://www.youtube.com/watch?v=5PesHXkN2M8
http://faculty.smu.edu/ttunks/projects/merrill/MarimbaH.html
https://www.youtube.com/watch?v=QZPyBDtoYc0
http://www.lafavre.us/tuning-marimba.htm

a) Modal Analysis

The "Trial and Error" method can then quickly lead to higher costs, particularly in the case of vibraphones, because of the material and more complex processing.

As engineers, we have therefore used modal analysis, a special form of structural dynamic simulation, which is possible with many commercially available CAD systems. The natural harmonics and the normal modes of oszillation of components with any geometry are calculated. The results can be displayed graphically.

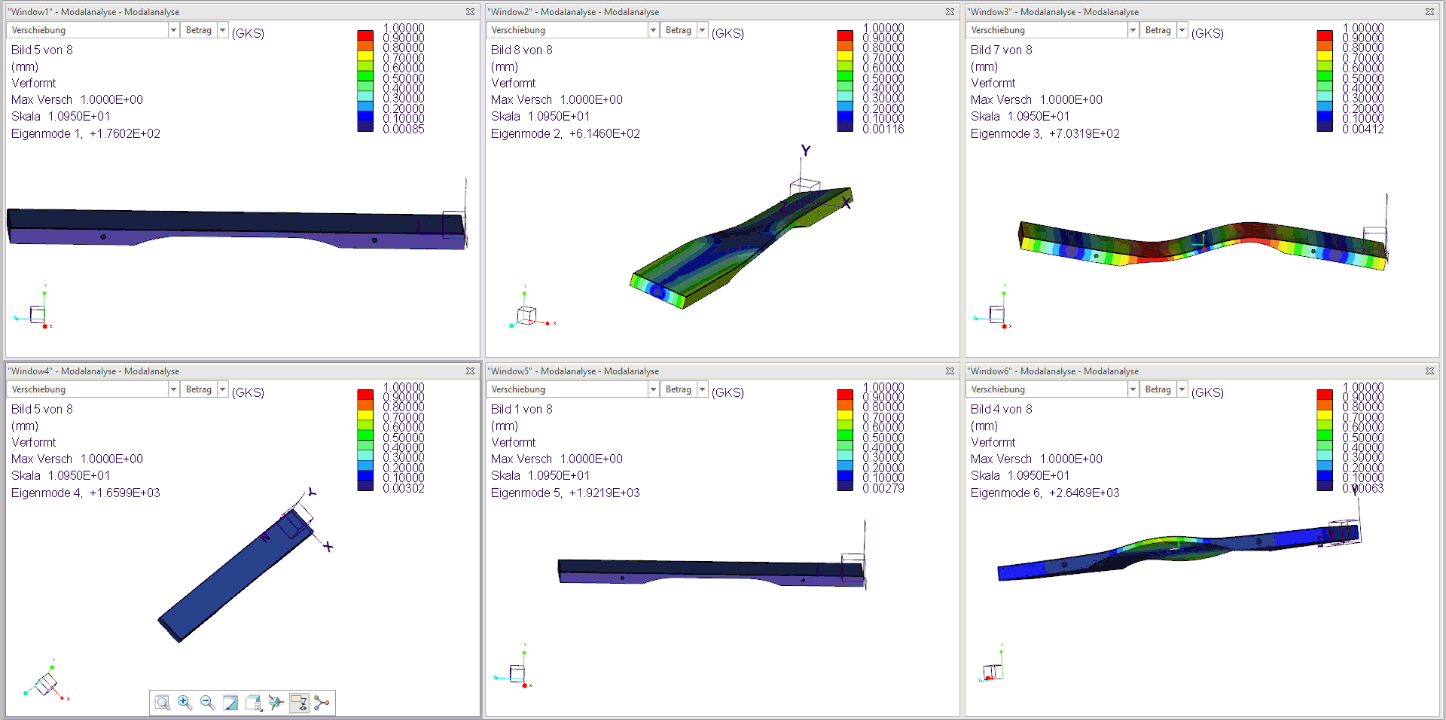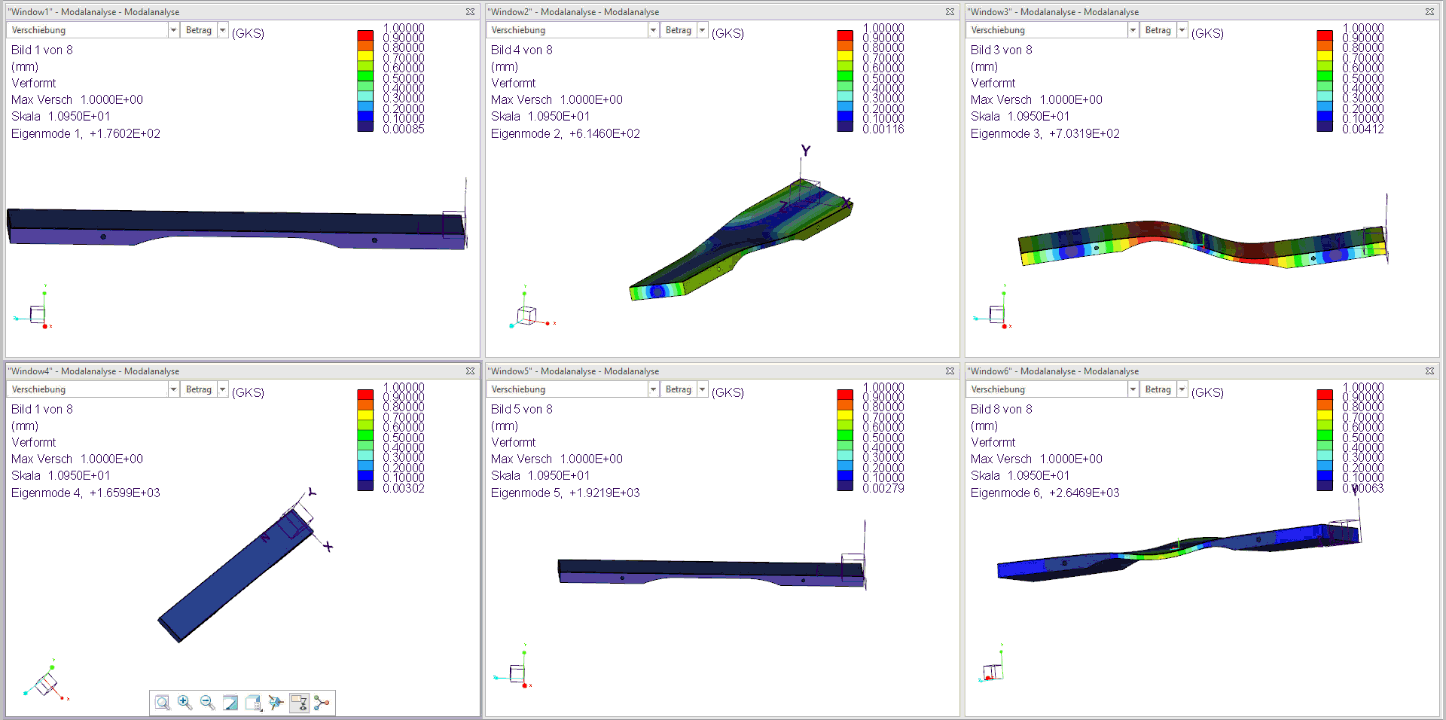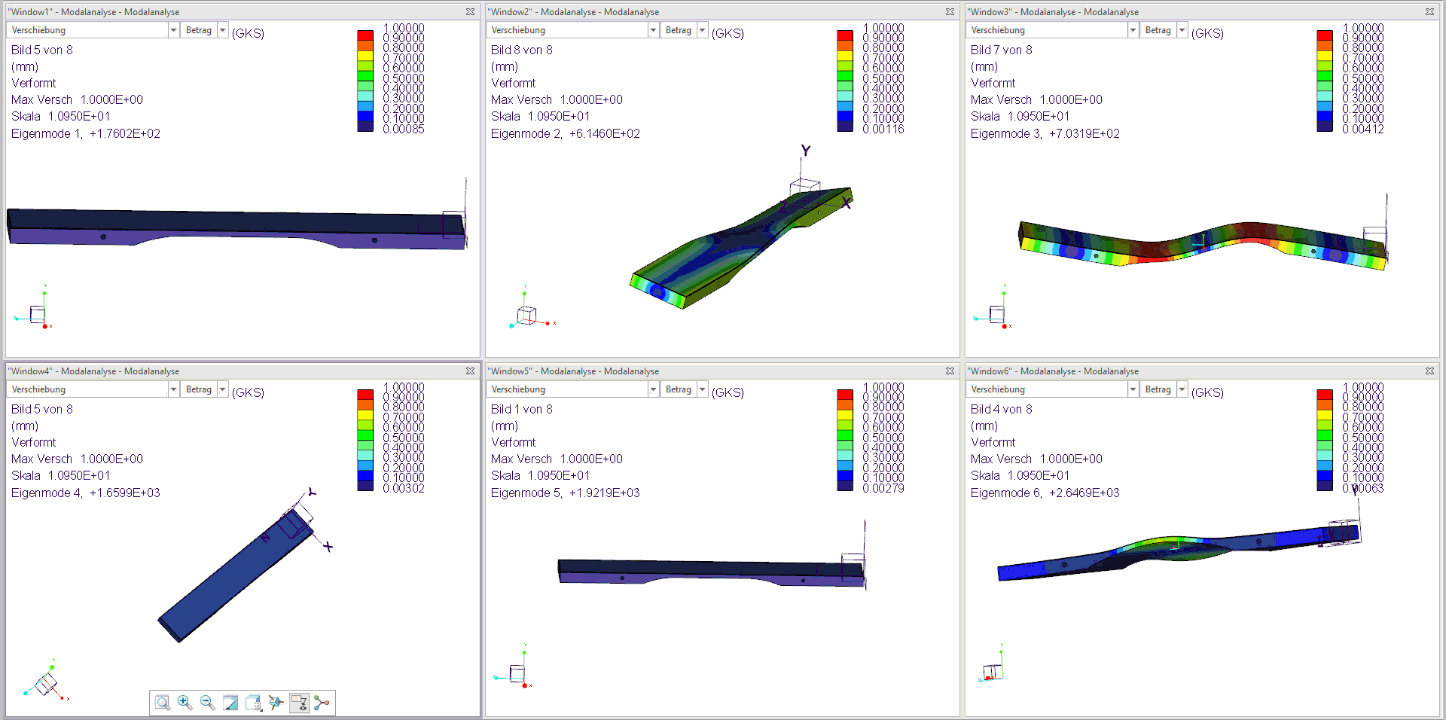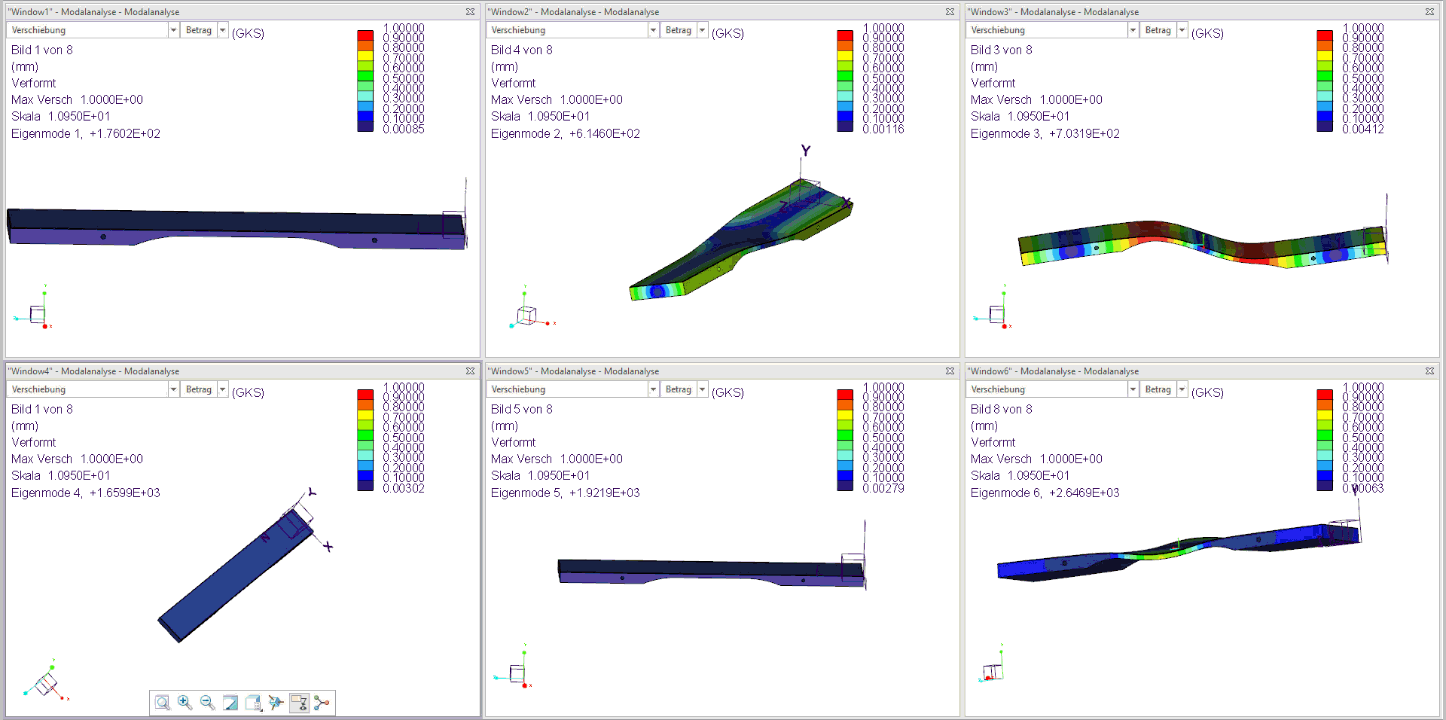
This enabled us to simulate each geometric shape (material removal) and compare the natural harmonics achieved, i.e. the sound spectrum, with our goal from step 1. We were also able to test which geometric change achieved which effect with regard to the natural harmonics.

The following figure shows the first 6 harmonics of an already tuned bar (F3):

The 3 tuned natural frequencies 1, 3 and 5 from the simulation therefore fulfill the sound goal from step 1 for the F3 bar with the basic frequency 176 Hz and 4 times the basic frequency (704 Hz). and 11 times the basic frequency (1936 Hz) very good!

We used the PTC simulation module for our modal analysis.
https://www.ptc.com/en/products/cad/creo/simulation-analysis/structural-analysis

 

b) First DIY Bar

There are a variety of ways to edit a rectangular bar so that a desired sound spectrum is achieved. For our first bar, we chose a somewhat unfortunate strategy that used the outer edges in addition to the central cutout. This bar was still tuned by hand with the file and the belt sander.

When placed on the frame, it was shown that the pedal damping had become inconsistent compared to the neighboring bars due to the processing on the edges. Nevertheless, this bar was a great success, since the concrete sound result matched our first simulation perfectly.

 

c) Tuning Geometry

We then determined our parametric tuning geometry from a variety of simulations:

First, the size (radius R, length L and depth T) of the central cutout is defined.

In the second step, the symmetrical lying tuning points A, described by the depth A, the position xA and the radius RA are defined.
We made sure that we placed the location xA in the nodes of the 5th harmonics.

In the third step, the central tuning point B, defined by the depth B and the radius RB, is defined.

With these 8 parameters, the tuning geometry is completely described for a given bar macro geometry.
In the case of the higher plates, the length L is omitted, since the two radii R grow together in the middle.

d) Simulation Quality

The many post-measurements have shown that our simulations were usually significantly less than 1% error compared to the actually milled bar.
Thus, the route through a simulated modal analysis is a very suitable approach.

 

e) Future Tuning Geometry

As already described in step 2, the surprisingly large tolerance range of the bars thickness (12.0 to 12.3 mm) caused us some problems, which meant that we had to measure all the bars individually before the modal analysis and ultimately - that's a lot worse - the analysis result can not be transferred to a next bar set.

For the next set of bars, we will therefore use thicker material (15 mm) and mill down on both sides precisely to our nominal thickness. Then we only need one set of simulations for all future bar sets that we may want to manufacture.