Step 3: Detailed geometry
Both the sound spectrum and the specific tone of the sound bars are achieved exclusively by removing material (milling, filing) from the underside of the sound bars. If the material is removed without achieving the desired sound, new material must be obtained.
There is some information on tuning sound bars in literature and on YouTube, but it is all rather vague.
Here are a few examples of links:
a) Modal Analysis
The "trial and error" method can quickly lead to higher costs, especially with the vibraphone, due to the material and more complex processing.
As engineers, we therefore used modal analysis, a special form of structural dynamic simulation that is possible with many commercially available CAD systems. This involves calculating the natural frequencies and natural vibration modes of a component with any geometry. The results can be displayed graphically. This allowed us to first simulate each geometric shape (material removal) and compare the resulting natural frequencies, i.e., the sound spectrum, with our target from step 1. We were also able to test which geometric changes had which effects on the natural frequencies.
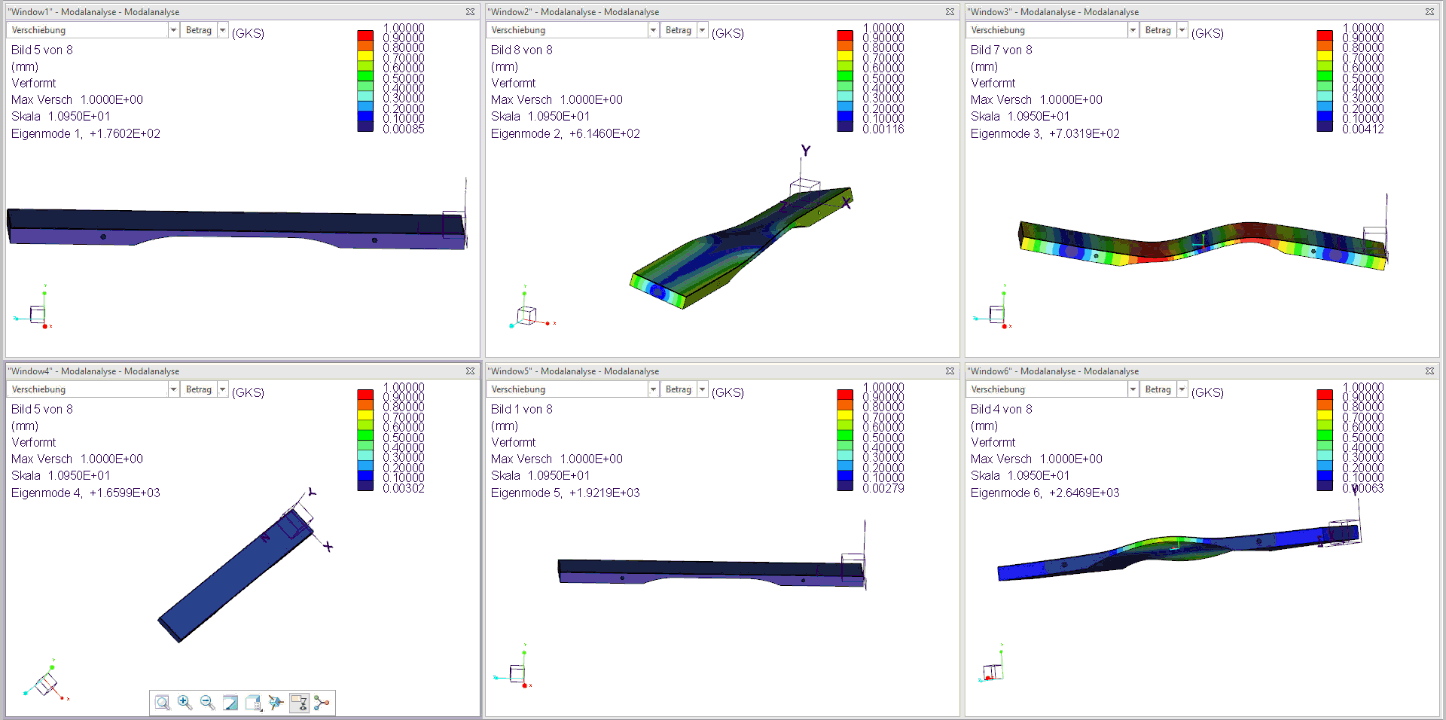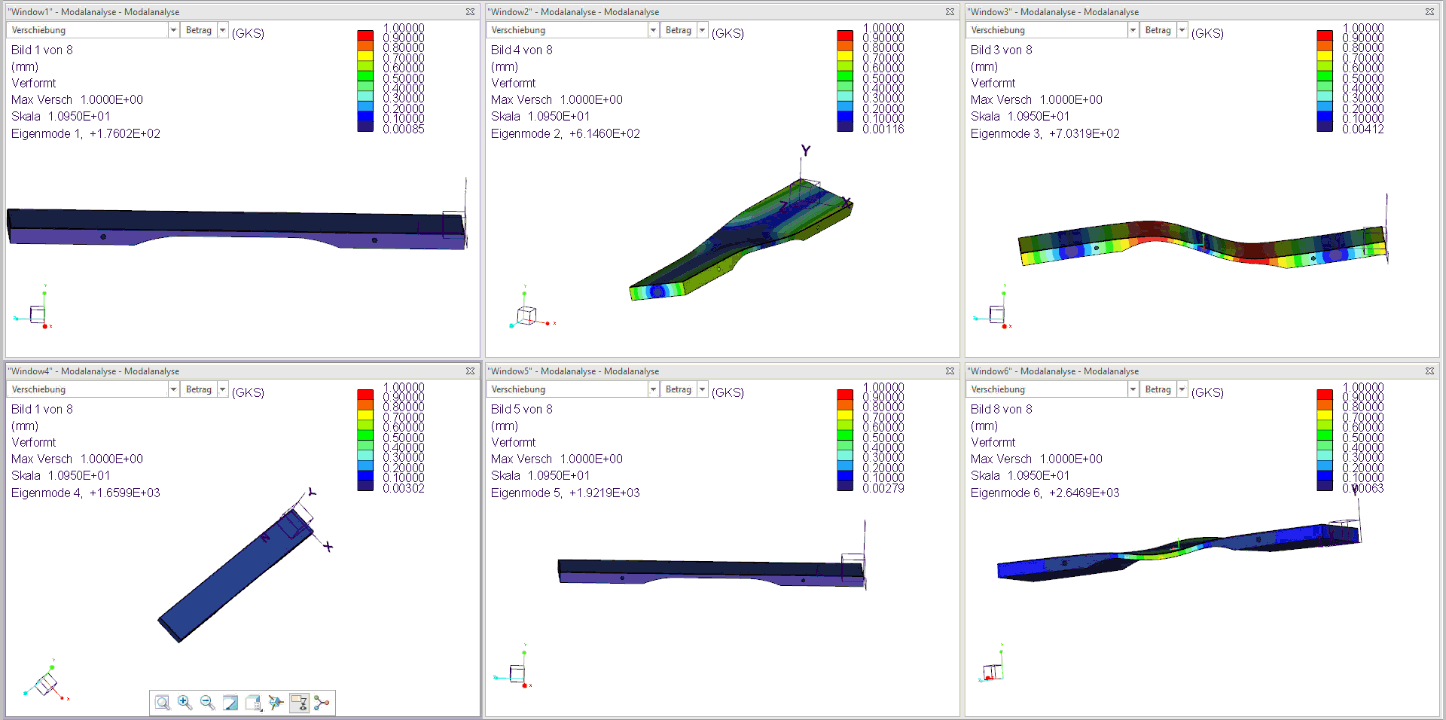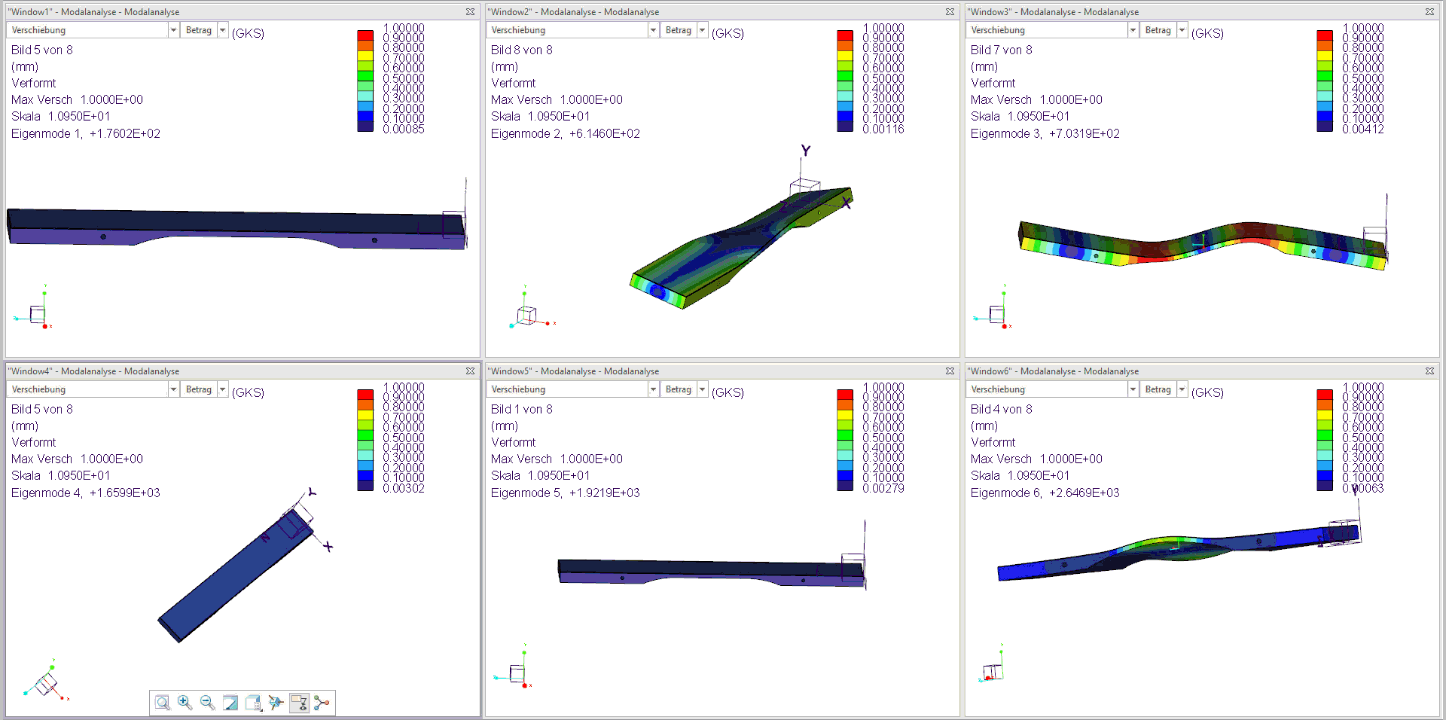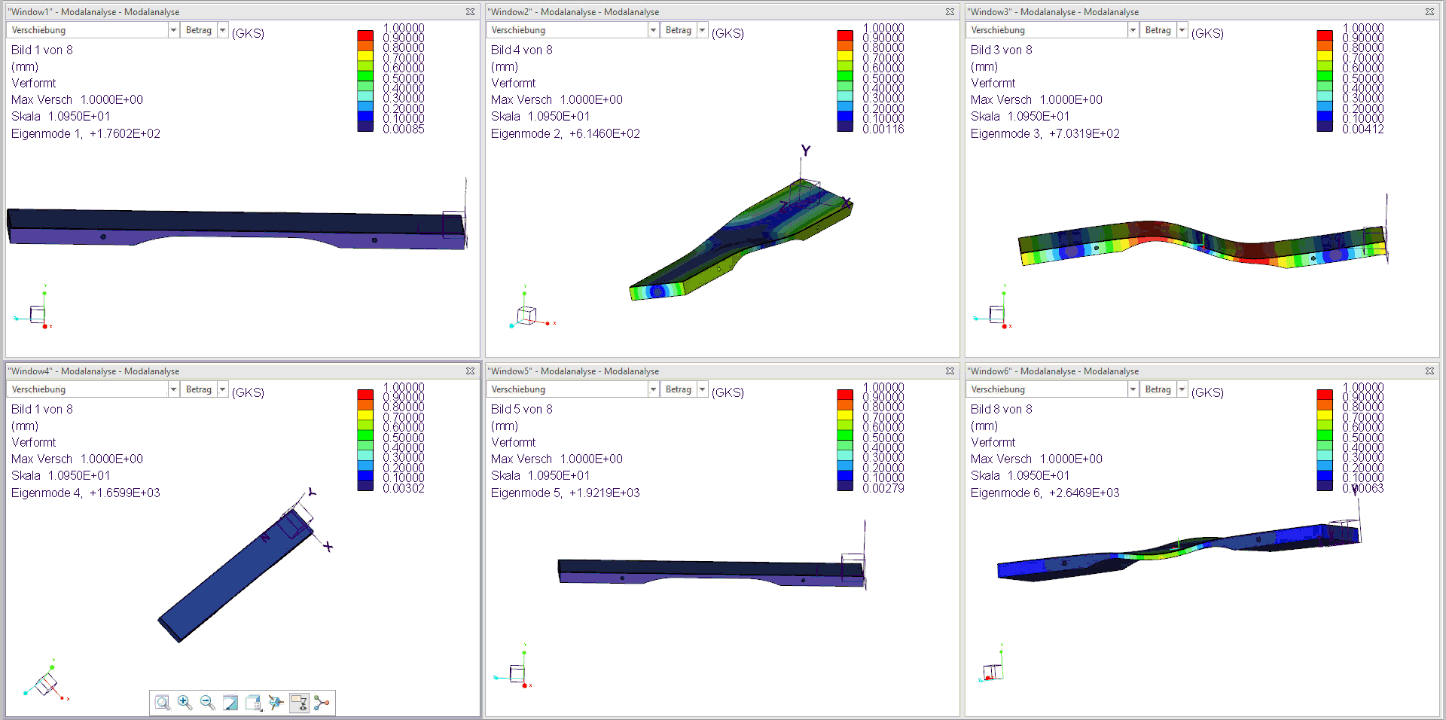
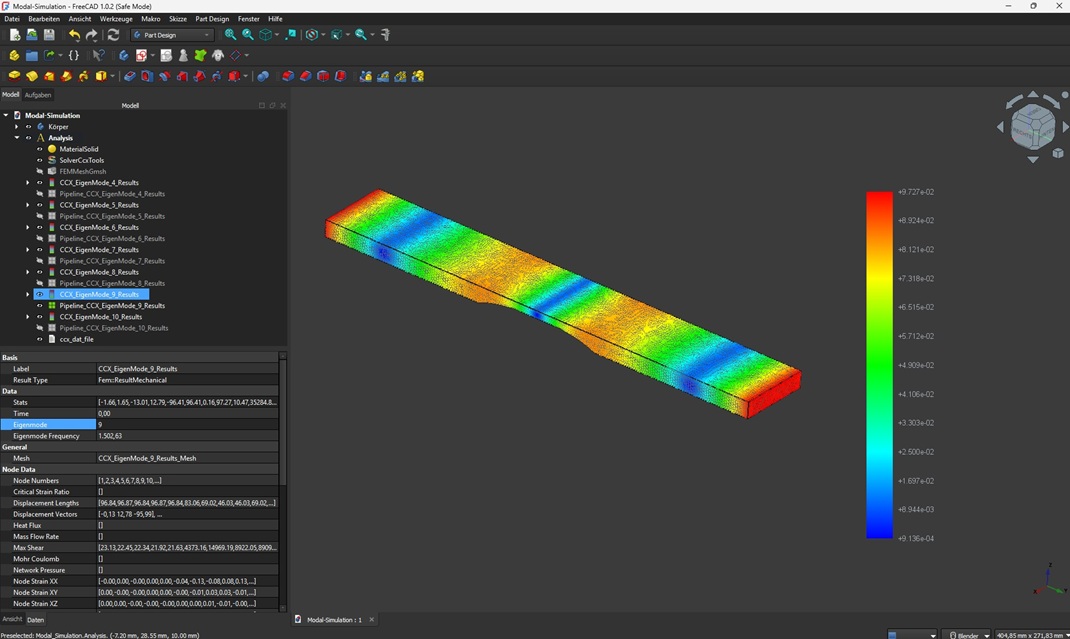
The figure below shows the first 6 natural modes of an already tuned sound plate (F3):
- Mode 2 is the torsional vibration of the sound bar, which occurs only with very small amplitude and is irrelevant to the sound.
- Mode 3 is the first harmonic, tuned here to 703 Hz.
- Mode 4 is the transverse vibration of the sound bar, which also occurs with very low amplitude and is irrelevant to the sound.
- Mode 5 is the second harmonic tuned here to 1922 Hz.
- Mode 6 is the second torsional vibration of the sound barand is also irrelevant.
The three tuned Modes 1, 3, and 5 from the simulation therefore meet the sound target from step 1 for the F3 bar with a fundamental frequency of 176 Hz and four times the fundamental frequency (704 Hz) as well as 11 times the fundamental frequency (1936 Hz) very well!
Simulation Software - Modal
For the modal analysis, we used PTC's simulation module at the university.
In fact, these calculations can also be performed using the free software FreeCAD, albeit in a slightly less convenient and more cumbersome manner. Tutorials on how to set up such a simulation can be found on the Internet, e.g. here.
The result of a FreeCAD modal simulation looks like this:
b) First Own Sound Bar
There are a variety of ways to process a rectangular sound bar in order to achieve the desired sound spectrum. For our first bar, we chose a somewhat unfortunate strategy that used the outer edges in addition to the central cutout in the middle of the plate. This bar was tuned by hand using a file (punishment work) and a belt sander.
When placed on the frame, it became apparent that the processing of the edges had caused the pedal damping to become uneven compared to the neighboring bars. Nevertheless, this bar was a great success, as the concrete sound result perfectly matched our initial simulation.
c) Tuning Geometry
We then determined our parametric tuning geometry from a large number of simulations:
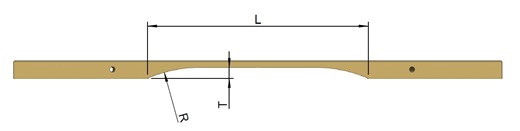
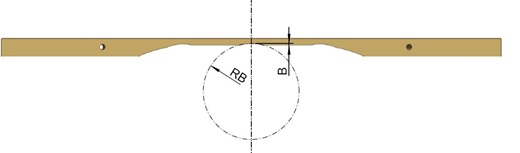
First, the size (radius R, length L, and depth T) of the central recess is defined as the basic geometry.
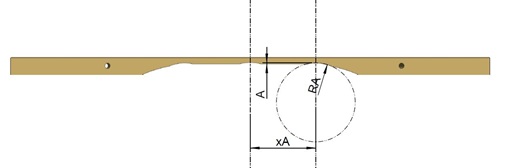
In the second step, the symmetrically located tuning points A, described by the depth A, the position xA, and the radius RA, are defined.
In doing so, we made sure to place the position xA at the nodes of the 5th mode.
These 8 parameters completely describe the tuning geometry for a given bar macrogeometry. For the higher bars, the length L is omitted because the two radii R converge in the middle.
d) Quality of the Simulation
The numerous follow-up measurements have shown that our simulations were usually well below 1% error compared to the actual milled sound bar.
This means that simulated modal analysis is a very suitable approach.
e) Future Tuning Geometry
As already described in step 2, the surprisingly large tolerance range of the bar thickness (12.0 to 12.3 mm) caused us some problems, which meant that we had to measure all bars individually and precisely before the modal analysis and, ultimately—which is much worse—we cannot transfer the analysis result to the next set of sound bars.
For the next set of bars, we therefore want to use thicker material (15 mm) and mill it down to our nominal thickness on both sides. Then we will only need one set of simulations for all future bars sets that we may want to manufacture.