Step 2: Plates - Macrogeometry
All readily available sound bar sets were in imperial dimensions, i.e., width increments of 2 1/4“, 2”, 1.75,“ and 1.5”. Therefore, our custom-built frames are also designed for these disc widths.
This meant that the width increments were fixed.
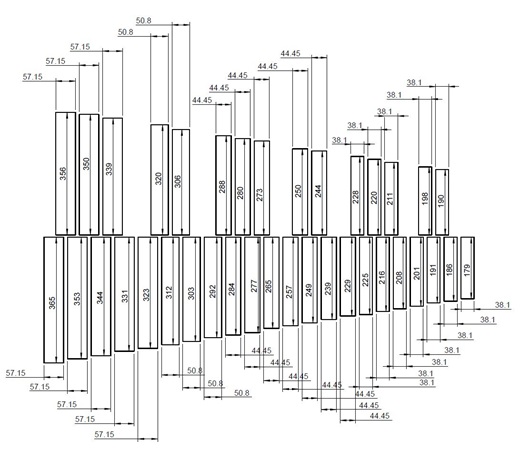
The same applied to the position of the cords, as these have to be guided through the frame. This meant that the bars lengths also had to correspond to the American model.
The board thickness of 1/2" = 12.7 mm commonly used in the USA was not available in Germany in the material we wanted. We were therefore faced with the alternative of milling the boards from 15 mm thick material or recalculating the tuning geometry to the next standard thickness of 12 mm.
| Due to the very limited availability of a suitable milling machine, we decided to have the bars widths cut out as strips from 12 mm thick standard panels. |
However, this has created two problems for us:
- On the one hand, the surfaces of the strips already have some damage (scratches, dents, etc.), which we then also have in the finished sound bar.
- Secondly, the panel thicknesses did exhibit considerable tolerances, ranging from 12.0 to 12.33 mm.
- When determining the required tuning geometry (modal analysis simulation), we found that even deviations of only 0.1 mm in the bar thickness have a very strong influence on the sound spectrum. Therefore, we had to measure each individual sound bar precisely after sawing and adjust the tuning geometry to the measured bar thickness.
As a result, we can only use the tuning geometry as determined for this specific set of bars.
What happens if you change the geometry specifications?
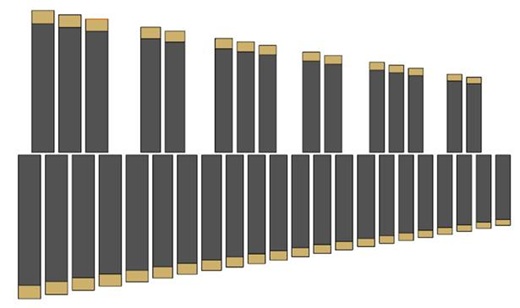
To find out, we investigated whether sound bars could be made from material only 10 mm thick in order to save weight. Because all possible youth vibraphones instead reduce the width of the sound bars, i.e., the scale length, we thought we would test a different approach.
In a simulation, we kept the scale length and thus the sound bar width in line with the American model so that the playing feel would remain unchanged, but then reduced the bar thickness to 10 mm. In order to return to the desired sound spectrum from step 1, we also had to reduce the bars lengths.
We have not yet simulated the entire set of sound bars, but we have checked the key points. The result is the set of sound bars shown in gray above the golden M55 bars.
This would result in a weight saving of around 1.3 kg, or almost 10% of the sound bars. The feel should be largely identical due to the consistent scale length, as should the sound spectrum.
The amplitude spectrum would be different, i.e., how strongly the individual overtone frequencies stand out from the others and the fundamental frequency.